[2.1] Euler 法
ここでは,Euler 法を用いた微分方程式の数値解法を Fortran プログラムで実装することを考えます.
[2.1.1] Euler 法で常微分方程式を解く
サンプルプログラム test1.f90 をダウンロードします.
$ wget www.ep.sci.hokudai.ac.jp/~inex/y2018/0706/practical/prog/test1.f90
test1.f90 は $\frac{df(z)}{dz}=-(z-a)f(z),\ a=3,\ f(0)=0.01$ という微分方程式を,$0\leq z\leq 10$の範囲で解くためのプログラムになっています.
test1.f90 の中身を見てみましょう.
$ less test1.f90
1 program main 2 3 implicit none 4 5 ! 定数・変数の宣言 --------------------------------------------- 6 double precision:: f_0 = 1.0d-2 ! f(z=0)の値 7 double precision:: z_max = 1.0d1 ! zの最大値 8 double precision:: dz = 1.0d-2 ! zの刻み幅 9 double precision:: a = 3.0d0 ! パラメータ 10 11 double precision:: z, f ! 変数 12 ! -------------------------------------------------------------- 13 14 open(10, file='data_z.dat') ! 出力ファイルを開く 15 16 ! 変数の初期値 ------------------------------------------------- 17 f = f_0 18 z = 0.0d0 19 write(10,*) z, f ! 初期値の出力 20 ! -------------------------------------------------------------- 21 22 ! ループ計算 (Euler法) ----------------------------------------- 23 do while (z <= z_max) 24 z = z+dz 25 f = f-(z-a)*f*dz 26 write(10,*) z, f 27 end do 28 ! -------------------------------------------------------------- 29 30 close(10) ! 出力ファイルを閉じる 31 32 end program main
このプログラムには,どこで何を行っているかを分かりやすくするためにコメント文を挿入しています.コメント文は! (エクスクラメーションマーク) から始まります.前回の hello.f90 と異なる点を大まかに記します:
- 5 行目から始まる変数等の宣言では,double precision というものが出てきています.これは,変数やパラメータが実数 (より正確には倍精度実数型) であることを宣言しています.Fortran の倍精度実数型では,$A\times 10^B$を$A$d$B$や$A$D$B$のように記します.
- 14, 30 行目では,出力ファイルの操作が記されています.14 行目のファイルを開く操作では,出力ファイル data_z.dat を指定し,ファイルに「10」という番号を割り当てています.これは機器番号と呼ばれるもので,出力先を表す番号です.この値はユーザーで指定することができます.30 行目では,機器番号 10 (すなわち出力ファイル data_z.dat) を閉じることが記述されています.
- 22 行目から始まるループ計算では,do-while 構文が用いられています.do-while 構文は,「ある条件が真の間,ずっと繰り返す」というもので,シェルスクリプトの while 文と同様の動作をします.ここでは,「変数 z が z_max 以下である (z <= z_max)」が真の間,計算を回し続けます.また,計算した z と f の値を,write 文を用いてファイル (機器番号 10 ) へ書き込んでいます.
それでは,このプログラムを GFortran でコンパイルし,実行してみましょう.
$ gfortran test1.f90 $ ./a.out
すると,データファイル (data_z.dat) が出力されます.
$ ls a.out data_z.dat test1.f90
このデータファイルの中身を見てみましょう.
$ less data_z.dat
0.0000000000000000 1.0000000000000000E-002 1.0000000000000000E-002 1.0299000000000001E-002 2.0000000000000000E-002 1.0605910200000001E-002 2.9999999999999999E-002 1.0920905732940000E-002 4.0000000000000001E-002 1.1244164542635025E-002 5.0000000000000003E-002 1.1575867396642759E-002 6.0000000000000005E-002 1.1916197898104056E-002 7.0000000000000007E-002 1.2265342496518505E-002 8.0000000000000002E-002 1.2623490497416845E-002 8.9999999999999997E-002 1.2990834070891676E-002 9.9999999999999992E-002 1.3367568258947535E-002 0.10999999999999999 1.3753890981631120E-002 0.11999999999999998 1.4150003041902096E-002 …… 略
1 列目に$z$,2 列目に$f(z)$が出力されていることがわかります.ここで,"E-002" が$10^{-2}$を表すことに注意してください.
得られた解をグラフに表してみましょう.グラフ描画のために gnuplot バッチファイルをダウンロードし,実行すると,微分方程式の解のグラフ (out1.pdf) が生成されます.
$ wget www.ep.sci.hokudai.ac.jp/~inex/y2018/0706/practical/prog/plot1.gpl $ gnuplot plot1.gpl
生成されたグラフ (out1.pdf) を見てみましょう.
$ firefox out1.pdf
グラフの横軸は$z$,縦軸は$f(z)$です.この微分方程式の解析解 ($f(z)=f(0)\exp\left\{-\frac{z^2-2az}{2}\right\}$) のグラフは,$z=3$に頂上がある山のような形をしています(Fig. 1).out1.pdf に表示される数値解は,特徴が一致しているでしょうか?また一致しない場所があるとすれば,どこでしょうか?
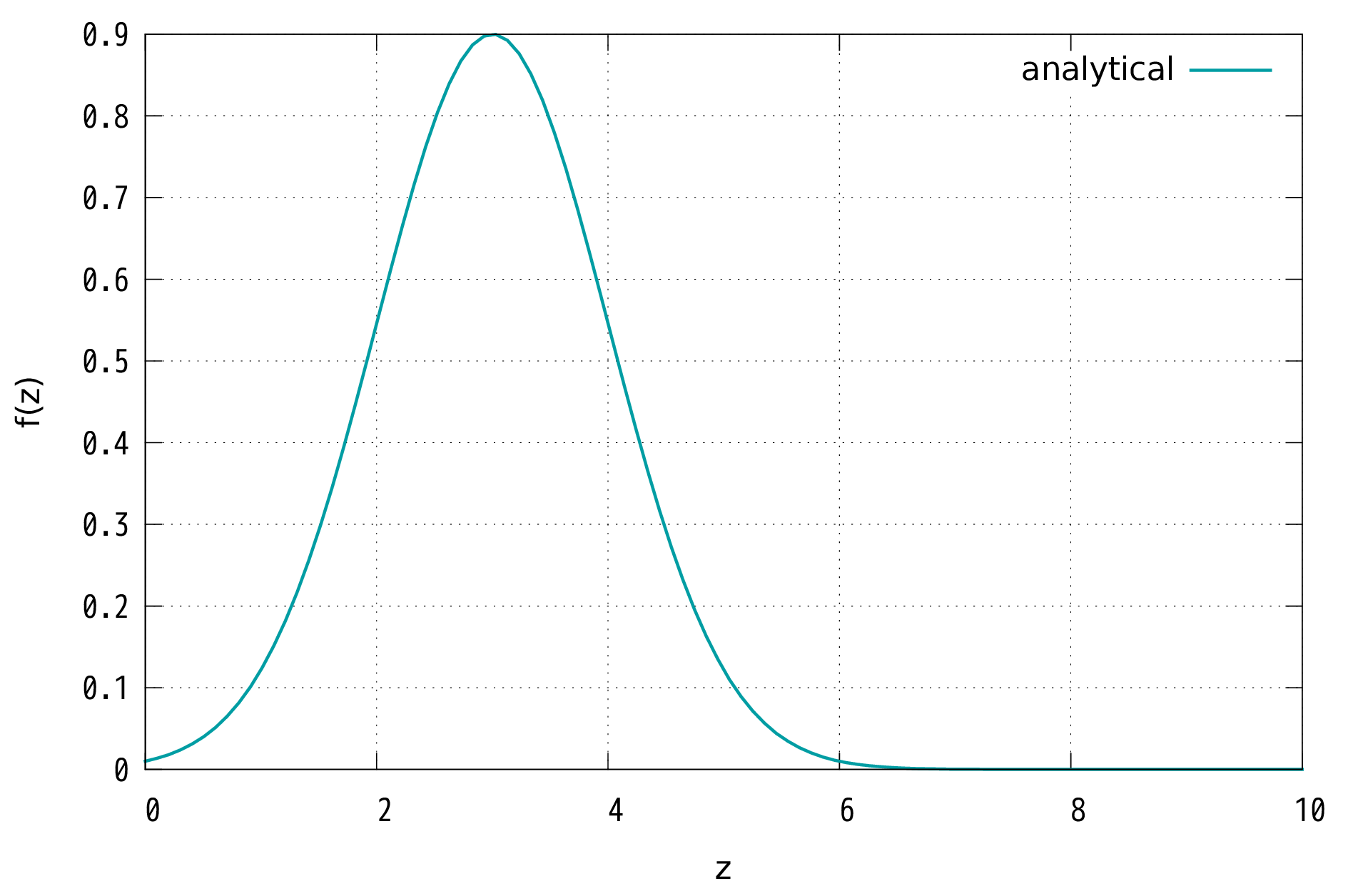
計算が成功していれば,これによく似た数値解のグラフが表示されるはずです.
なお,plot1.gpl を vi で開き,コメントアウトのマーク (行頭の"#") を消して plot1.gpl を再度実行すると,数値解のグラフと合わせて解析解のグラフも表示され,数値解と解析解の比較ができます.余裕がある人はこれらがどの程度一致しているかを確かめてみましょう.このとき,ou1.pdf を開いたまま gnuplot を実行しても,ファイルが更新されません.out1.pdf を閉じた状態で gnuplot を実行するようにしてください.
[2.1.2] Euler 法で運動方程式を解く
ここまでは1階微分方程式を解く例を見てきましたが,自然界に現れる方程式の多くは運動方程式であり,これは基本的に2階微分方程式です.ここでは,運動方程式を解くサンプルプログラムを見てみます.
サンプルプログラム test2.f90 をダウンロードします.
$ wget www.ep.sci.hokudai.ac.jp/~inex/y2018/0706/practical/prog/test2.f90
このプログラムは,太陽周りの天体の運動を計算するためのプログラムで, \begin{align} &\frac{d^2 x}{dt^2}=-\frac{GM}{r^2}\frac{x}{r},\\ &\frac{d^2y}{dt^2}=-\frac{GM}{r^2}\frac{y}{r},\\ &r=\sqrt{x^2+y^2},\\ \end{align} という微分方程式を解いています.ここで,$x,y$は太陽を中心とした天体の座標位置,$r$は太陽からの距離,$G$は万有引力定数,$M$は太陽質量です.このプログラムでは,天体の初期位置は太陽から 1 AU 離れたところにあり,公転速度も地球とほぼ同じとしているため,軌道はほぼ地球と同じ円軌道となります.
ここで,test2.f90 の中身を見てみましょう.
$ less test2.f90
1 program main 2 3 implicit none 4 5 ! 定数・変数の宣言 --------------------------------------------- 6 double precision:: M = 1.9884D30 ! 太陽質量 [kg] 7 double precision:: G = 6.67408D-11 ! 万有引力定数 8 9 double precision:: t_max = 2.0D0*3.1536D7 ! 時間の最大値 (2年) 10 double precision:: dt = 1.0D3 ! 時間の刻み幅 (1000sec) 11 12 double precision:: x, y, u, v, t, r ! 変数 13 double precision:: uu, vv ! 変数 14 ! -------------------------------------------------------------- 15 16 open(10, file='data_planet.dat', status='replace') ! 出力ファイルを開く 17 18 ! 変数の初期値 ------------------------------------------------- 19 t = 0.0D0 20 x = 1.496D11 ! 1AU 21 y = 0.0D0 22 u = 0.0D0 23 v = 2.9788D4 ! 29.8km/sec 24 write(10,*) t, x, y ! 初期値の出力 25 ! -------------------------------------------------------------- 26 27 ! ループ計算 (Euler法) ----------------------------------------- 28 do while (t <= t_max) 29 uu = u 30 vv = v 31 32 t = t+dt 33 34 r = sqrt(x*x+y*y) 35 u = u-G*M*x/(r*r*r)*dt 36 v = v-G*M*y/(r*r*r)*dt 37 38 x = x+uu*dt 39 y = y+vv*dt 40 write(10,*) t, x, y 41 end do 42 ! -------------------------------------------------------------- 43 44 close(10) ! 出力ファイルを閉じる 45 46 end program main
Euler 法をはじめとする数値積分法では,2階の微分方程式を連立した2つの1階微分方程式に直して解きます.例えば,今回の運動方程式では, \[\frac{d^2x}{dt^2}=-\frac{GM}{r^2}\frac{x}{r}\longrightarrow \frac{dx}{dt}=u,\ \frac{du}{dt}=-\frac{GM}{r^2}\frac{x}{r}\] というふうに,速度変数$u$を用いれば2つの1階微分方程式に直すことができます.この test2.f90 のループ計算部分でも,u (速度の$x$成分), v (速度の$y$成分) を導入して2階微分方程式を連立1階微分方程式に直し,それを Euler 法で計算するという手順が見て取れます.
それでは,このプログラムをコンパイル・実行してみましょう.
$ gfortran test2.f90 $ ./a.out
すると,データファイル (data_planet.dat) が出力されます.得られたデータを可視化するために,gnuplot バッチファイル (plot_planet_orbit.gpl) をダウンロードし,gnuplot を実行します.
$ wget www.ep.sci.hokudai.ac.jp/~inex/y2018/0706/practical/prog/plot_planet_orbit.gpl $ gnuplot plot_planet_orbit.gpl
これにより,グラフ (out_planet.pdf) が出力されますので,firefox で閲覧してみましょう.
$ firefox out_planet.pdf
このグラフでは中心に太陽位置が描かれ,横軸は位置座標$x$,縦軸は位置座標$y$で,惑星軌道を見下ろすような視点で見ることになります.太陽の周りを円を描いて回る軌道は得られたでしょうか? また,数値解は厳密には円軌道を描かないはずです.円軌道との違いは何でしょうか? なお,vi 等で plot_planet_orbit.pdf を開き,コメントマーク部を消去して再度 gnuplot を実行すれば,解析解もグラフに表示されるようになります.解析解は円軌道を表現するため,円軌道との違いが明瞭になります.
[2.1.3] 計算パラメータの変更
test2.f90 の初期条件や変数の値を書き換えると,様々な天体の軌道の計算ができます.例題1では,惑星探査機を例に,初期条件を変えて様々な軌道を計算してみましょう.また,Euler法をはじめとする数値積分では,計算で用いる変数の値を適切に設定しないと,思うような計算精度が得られないことがあります.例題2では,計算で用いる変数の値を変更し,数値解が正しく解を表現できない例を見てもらいます.
例題1:惑星探査機の軌道計算
惑星探査機の軌道を計算してみましょう.地球から打ち上げることを考え,初期位置は元のままに,初速度を変更することにします.この計算は,惑星たちからの重力を無視し,太陽の重力のみを考えて探査機の軌道を導くものになります(このような計算設定は,惑星探査機で要求される推進剤質量を概算する際によく用いられます).ここで探査機の初速度を地球の速度 ( = 約29.8 km/s,元の速度) から数 % 上下させるとき,探査機が火星軌道/金星軌道と交差するのは何 % 変えたときでしょうか?実際に 23 行目で v の値を書き換えて確かめてみましょう.
探査機の軌道解析用のプログラムを用意し,これを explorer.f90 とします.
$ cp test2.f90 explorer.f90
精度を上げるため,explorer.f90 の 10 行目で,時間の刻み幅 dt を,100 (=1.0D2) 秒と書き換えます.
double precision:: dt = 1.0D2
まず,速度を 3% 上昇させてみましょう.explorer.f90 の 23 行目の v の欄を以下のようにします.
v = 1.03D0*2.9788D4
これは,元の速度を 1.03 倍するという意味です.変更したら,コンパイルし,実行ファイルを実行します.
$ gfortran explorer.f90 $ ./a.out
グラフ描画のバッチファイルは,新しいファイル (plot_planet_orbit2.gpl) をダウンロードして使いましょう.
$ wget www.ep.sci.hokudai.ac.jp/~inex/y2018/0706/practical/prog/plot_planet_orbit2.gpl $ gnuplot plot_planet_orbit2.gpl
このバッチファイルを使ってグラフ (out_planet2.pdf) を出力すると,先ほどのグラフと同様の座標系で他の惑星の軌道も描かれるため,惑星軌道への到達の判定に便利です.
軌道交差が起こるためには±10 % 以下の速度変化で充分です.なので,全てを逐一確かめるのではなく,「アタリ」をつけて計算を実行しましょう.
例題2:Euler 法の計算誤差
Euler 法で運動方程式を計算した結果では,誤差が積み重なってエネルギーが厳密には保存しません.例えば今回の場合,エネルギーは単調に増加してしまい,計算上,地球がどんどん太陽から離れてしまいます.この影響は,時間刻みを大きく取ったときに顕著です.ここでは,時間刻みで誤差が積み重なる様を見てみましょう.
解析用のプログラムを用意し,これを err.f90 とします.
$ cp test2.f90 err.f90
誤差の影響を分かりやすくするため,err.f90 の9行目で,時間の最大値を10年に書き換えます.
double precision:: t_max = 1.0D1*3.1536D7
ここで,10行目を書き換え,時間の刻み幅を 1000秒 (1.0D3) から,1万秒 (1.0D4),10万秒 (1.0D5),100万秒 (1.0D6) とします.例えば,1万秒に書き換える場合は,変数 dt の定義行 (10行目) を以下のようにします.
double precision:: dt = 1.0D4
書き換えたら,計算実行・グラフ描画をしてみましょう.グラフ描画には,先ほどの plot_planet_orbit2.gpl を用いてください.
$ gfortran err.f90 $ ./a.out $ gnuplot plot_planet_orbit2.gpl
例えば,地球が 10 年以内に火星軌道以遠まで弾き飛ばされてしまうような時間刻みはどれくらいでしょうか? Euler 法によるエネルギー増大を味わってみてください.また,すべて終わって時間が余った人は,付録にチャレンジしてみましょう.
[2.1.4] 付録:静水圧平衡の式のプログラムを書いてみよう
サンプルプログラムの「定数・変数の宣言」と「変数の初期値」,「ループ計算」の部分を適切に書き換えれば,色々な微分方程式を解くことができるようになります. test1.f90 を,大気圧の鉛直プロファイルが満たす微分方程式(静水圧平衡の式): \[\frac{dp(z)}{dz}=-\frac{mg}{kT}p(z)\] を解くためのプログラムへと書き換えてみましょう.ここで,$p(z)$は高度$z$における大気圧,$m$は大気分子の平均質量,$g$は重力加速度,$k$はBoltzmann定数,$T$は大気の温度[K]です.解く際には,高度範囲は$0\sim 10^4\,\mathrm{m}$,高度刻み ($dz$) は$1000\,\mathrm{m}$としましょう.なお,書き換えに当たっては以下の定数を用いてください.
- 地表面気圧:$p_0=p(z=0)=1.01325\times 10^{5}\,\mathrm{Pa},$
- 大気分子の平均質量:$m=4.80990\times 10^{-26}\,\mathrm{kg},$
- 重力加速度:$g=9.80665\,\mathrm{m/s^2},$
- Boltzmann定数:$k=1.38065\times 10^{-23}\,\mathrm{m^2\cdot kg/(s^2\cdot K)},$
- 温度:$T=288\,\mathrm{K}$
書き換えが終わったら,プログラムを実行して,データファイル (data_z.dat) を生成してみましょう.
$ gfortran test1.f90 $ ./a.out
データファイルを生成したら,gnuplot バッチファイル (plot_atm_profile.gpl) をダウンロードしてグラフ (out_atm_profile.pdf) を描き,それを表示しましょう.
$ wget www.ep.sci.hokudai.ac.jp/~inex/y2018/0706/practical/prog/plot_atm_profile.gpl $ gnuplot plot_atm_profile.gpl $ firefox out_atm_profile.pdf
このグラフは,縦軸が高度$z$,横軸が大気圧$p(z)$です.高度とともに大気圧が指数関数的に減少する姿が観察できるでしょうか?解析解と数値解を比較したい人は,plot_atm_profile.gpl のコメントマークを消去してもう一度グラフを生成してみてください.
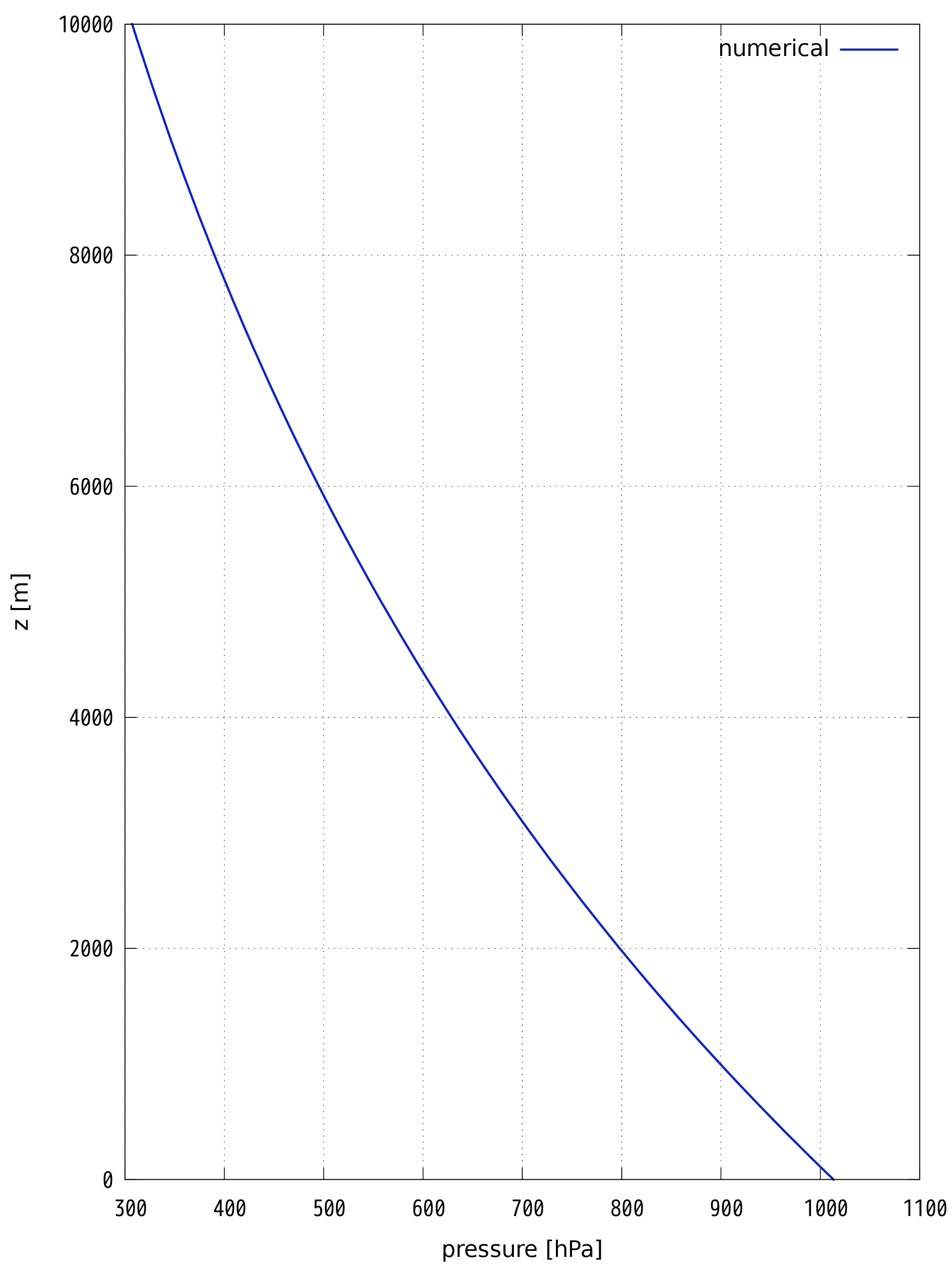
これと同じグラフが得られましたか?