相空間による運動の記述

ハミルトニアンの物理学的意味

デカルト座標系のNewton力学よろしく、$K=\frac{p^2}{2m},p=m\dot{q}$と表現されるなじみ深い場合を考えてみよう。この場合は、$p\dot{q}=2K$となるため、ハミルトニアン$H$は、 \[H=p\dot{q}-L=2K-K+U=K+U\] となる。以下に見るように、一般に、Hamiltonの（運動）方程式に従う系は、時間発展に対してハミルトニアンが不変量となる。これらのことからわかるように、ハミルトニアンは系の力学的エネルギーの一般化になっている。ただし、ハミルトニアンは位置と運動量からエネルギーを返す関数（写像）であって、エネルギーそのものではないことに注意する。

相空間とトラジェクトリ

系の状態を$(\{q_i\},\{p_i\})$という点を集めた$2N$次元の空間で表現するのはごく自然なことである。この、$q,p$で張られる空間を相空間(Phase space)という（位相空間と呼ぶ場合もあるが、数学の位相空間:topological spaceと混同する可能性があるので、相空間と呼ぶ）。系の状態は相空間の一点に相当し、系の時間発展は点の移動によって行われる。このときの、相空間上の点の軌跡をトラジェクトリ(Trajectory)と呼ぶ。

先に少し紹介した通り、ハミルトニアンは時間不変量である。このことは、Hamiltonの方程式に従う力学系が描くトラジェクトリが相空間上のハミルトニアンの等値線になることを意味し、相空間上のハミルトニアンの勾配ベクトル$\overrightarrow{\mathrm{grad}}_p H$とトラジェクトリの線素ベクトル$d\vec{z}$が直交することから分かる。2次元相空間で計算すれば、 \begin{align} \overrightarrow{\mathrm{grad}}_p H\cdot d\vec{z}&=\left(\frac{\partial H}{\partial q},\frac{\partial H}{\partial p}\right)\cdot(dq,dp)\notag\\ &=\left(\frac{\partial H}{\partial q},\frac{\partial H}{\partial p}\right)\cdot\left(\frac{dq}{dt},\frac{dp}{dt}\right)dt\notag\\ &=\left(\frac{\partial H}{\partial q},\frac{\partial H}{\partial p}\right)\cdot\left(\frac{\partial H}{\partial p},-\frac{\partial H}{\partial q}\right)dt&\text{(Hamiltonの方程式より)}\notag\\ &=0.\notag \end{align} となる。この式変形から分かる通り、ハミルトニアンの時間不変性はHamiltonの方程式にすでに組み込まれており、方程式に内在する対称性なのである。

系が完全にHamiltonの方程式に従っている限り、ハミルトニアンの保存性は保証される。Hamilton系が保存系とも呼ばれるのはこの性質に由来する。Hamilton系では、系の時間発展を表すトラジェクトリの方程式の決定は簡単である。ハミルトニアン$H$は、$q_i,p_i$に依存する関数なので、陰関数曲線$H(\{q_i\},\{p_i\})=\epsilon=\mathrm{const}.$を考えればよい。しかしながら、ハミルトニアンが時間不変であっても、現実の力学系がそれに沿った運動をするかは別問題である。たとえばNewton力学では、力学的エネルギー以外の寄与を考えたとき、今考えているハミルトニアンで考慮していない因子（たとえば熱エネルギー）が生じ、ハミルトニアンの保存性を壊してしまう。このような系を非保存系という。非保存系のトラジェクトリの決定は、熱エネルギー等の非保存的因子の寄与に応じて$\epsilon$を可変パラメータとすることで得られる。これ以降、特に断りがなければHamilton系を扱う。

Hamilton系では、相空間中の一点を定めることはある時刻における運動状態を一意に定めることに等しいことに注意する．ある時刻で相空間内の一点が定められたとき、それ以降の運動は一意的に決定される。つまり、ある点から延びるトラジェクトリは一意的に定められ、分岐したり交わったりすることはない。しかし、ある特殊な状況においては、トラジェクトリが交わったり分岐するような点が現れる。これを、特異点(Singularity)と呼ぶ。相空間上の点の流れを考えたとき、特異点はその不動点である。すなわち、特異点を初期条件に持つ運動はその力学的状態が不変となる。

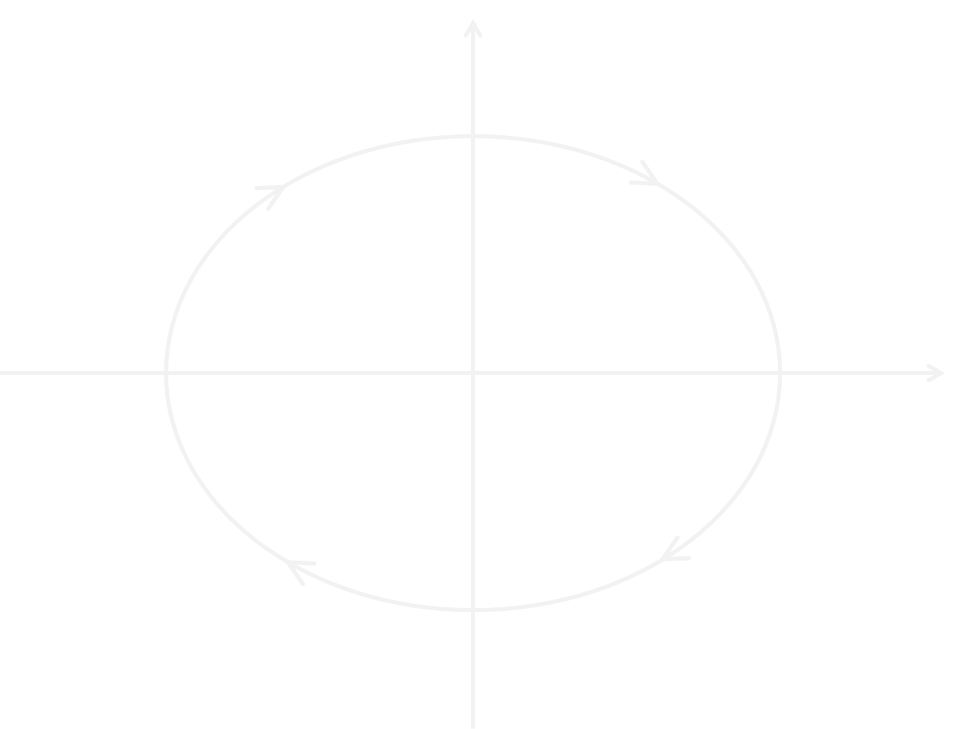
例：調和振動子のトラジェクトリ

保存系における、ばね定数$k$の調和振動子のハミルトニアンは、 \[H=\frac{p^2}{2m}+\frac{1}{2}kx^2=\epsilon=\mathrm{const.}\] で与えられる。両辺を$\epsilon$で割って整理すれば、 \[\frac{1}{2m\epsilon}p^2+\frac{k}{2\epsilon}x^2=1\] となる。これは楕円の方程式を表し、調和振動子は相空間上で楕円の軌道を描くような時間発展をすることがわかる（Fig.1）。

Fig. 1 調和振動子のトラジェクトリ。
矢印の向きは時間発展での点の移動方向を表す。

流体力学との対応

状態点がトラジェクトリ上を駆け抜ける速さ$d\vec{z}/dt$についてもう少し考察を深めよう。先の議論から、 \[\frac{d\vec{z}}{dt}=\left(\frac{\partial H}{\partial p},-\frac{\partial H}{\partial q}\right)\] であり、これはハミルトニアンの勾配に直交する。さらに言えば、ただ直交するだけでなく、これは勾配ベクトルをそのまま90度回転させたものになっている。ハミルトニアンの勾配ベクトルはハミルトニアンの等値線の個数密度と考えることができるため、ハミルトニアンの等値線が密集しているところでは、点は相空間上で速く移動するといえる。

勾配ベクトルと速度ベクトルの直交性・スケール性は、気象学における等圧面（等圧線）と風（特に地衡風）の関係や、流体力学における速度と速度ポテンシャルの関係の類似物になっていて、ハミルトニアンは状態点の流れ場の速度ポテンシャルであるとも言うことができる。この視座は、Hamilton系を流体力学の言葉を使って再定式化するというよりも、むしろ流体の問題をHamilton系で扱える可能性を示す点で意義深い。このことの詳細は「流体力学のHamilton形式」（未着手）で取り上げることにする。

最後に、もう一つ、Hamilton力学と流体力学との類似物を見てみることにする。状態点の速度ベクトルを相空間全体で束ね、それを流れ場と見たとき、この発散は0になるという著しい性質がある： \begin{align} \mathrm{div}_p\left(\frac{dq}{dt},\frac{dp}{dt}\right)&=\mathrm{div}_p\left(\frac{\partial H}{\partial q},-\frac{\partial H}{\partial p}\right)\notag\\ &=\frac{\partial}{\partial q}\frac{\partial H}{\partial p}-\frac{\partial}{\partial p}\frac{\partial H}{\partial q}\notag\\ &=0\notag \end{align} これは、粒子集団で張られた相空間内の有限体積が、時間不変となることを意味している（Liouvilleの定理）。この定理は、粒子集団を物理量の分布関数として扱う統計力学において応用が深い。一方、流体力学とのアナロジーとしては、Liouvilleの定理は、相空間内で粒子集団が非圧縮性流体のようにふるまうことを暗示している。

Copyright (C) Matsuoka Ryo All Rights Reserved.
Last update: 2020/06/04